




Next: Example (from Program LA_SBGVX_EXAMPLE)
Up: Generalized Symmetric Eigenvalue Problems
Previous: Purpose
Contents
Index
- AB
- (input/output) REAL or COMPLEX
array, shape
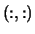 with
with 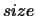 (AB,1)
(AB,1) 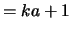 and
and
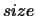 (AB,2)
(AB,2) 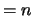 ,
where
,
where 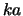 is the number of subdiagonals or superdiagonals in the
band of
is the number of subdiagonals or superdiagonals in the
band of 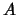 and
and 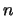 is the order of
is the order of 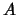 and
and 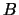 .
.
On entry, the upper (if UPLO = 'U') or lower
(if UPLO = 'L') triangle of 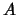 in band storage. The
in band storage. The
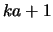 diagonals of
diagonals of 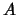 are stored in the rows of AB so that the
are stored in the rows of AB so that the
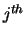 column of
column of 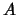 is stored in the
is stored in the 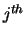 column of
column of
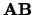 as follows:
as follows:
On exit, the contents of AB are destroyed.
- BB
- (input/output) REAL or COMPLEX
array, shape
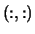 with
with 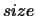 (BB,1)
(BB,1) 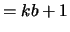 and
and
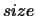 (BB,2)
(BB,2) 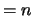 , where
, where 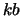 is the number of subdiagonals or
superdiagonals in the band of
is the number of subdiagonals or
superdiagonals in the band of 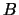 .
.
On entry, the upper (if UPLO = 'U') or lower
(if UPLO = 'L') triangle of matrix
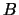 in band storage.
The
in band storage.
The 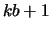 diagonals of
diagonals of 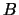 are stored in the rows of
BB so that the
are stored in the rows of
BB so that the 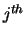 column of
column of 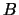 is
stored in the
is
stored in the 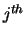 column of
column of 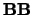 as
follows:
as
follows:
On exit, the factor 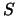 from the split Cholesky
factorization
from the split Cholesky
factorization 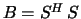 .
.
- W
- (output) REAL array, shape
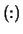 with
with
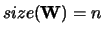 .
.
The first M elements contain the selected eigenvalues in
ascending order.
- UPLO
- Optional (input) CHARACTER(LEN=1).
![\begin{optionarg}
\item[{$ =$\ 'U':}] Upper triangles of $A$\ and $B$\ are stor...
...item[{$ =$\ 'L':}] Lower triangles of $A$\ and $B$\ are stored.
\end{optionarg}](img791.gif)
Default value: 'U'.
- Z
- Optional (output) REAL or
COMPLEX square array, shape
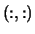 with
with
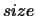 (Z,1)
(Z,1) 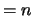 .
.
The first M columns of Z contain the orthonormal
eigenvectors corresponding to the selected eigenvalues, with
the i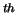 column of Z containing the
eigenvector associated with the eigenvalue in W
column of Z containing the
eigenvector associated with the eigenvalue in W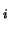 .
The eigenvectors are normalized so that
.
The eigenvectors are normalized so that 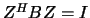 .
If an eigenvector fails to converge, then
that column of Z contains the latest approximation to the
eigenvector and the index of the eigenvector is returned in
IFAIL.
.
If an eigenvector fails to converge, then
that column of Z contains the latest approximation to the
eigenvector and the index of the eigenvector is returned in
IFAIL.
- VL,VU
- Optional (input) REAL.
The lower and upper bounds of the interval to be searched
for eigenvalues. VL 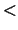 VU.
VU.
Default values:
VL 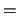 -HUGE(wp) and VU
-HUGE(wp) and VU 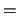 HUGE(wp),
where wp ::= KIND(1.0)
HUGE(wp),
where wp ::= KIND(1.0) 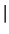 KIND(1.0D0).
KIND(1.0D0).
Note: Neither VL nor VU may be present if IL
and/or IU is present.
- IL,IU
- Optional (input) INTEGER.
The indices of the smallest and largest eigenvalues to be
returned. The 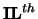 through
through 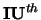 eigenvalues
will be found.
eigenvalues
will be found.
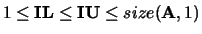 .
.
Default values: IL 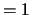 and IU
and IU 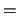
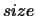 (A,1).
(A,1).
Note: Neither IL nor IU may be present if VL and/or VU
is present.
Note: All eigenvalues are calculated if none of the arguments VL, VU,
IL and IU are present.
- M
- Optional (output) INTEGER.
The total number of eigenvalues found.
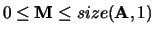 .
.
Note: If 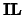 and
and 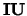 are present then
are present then
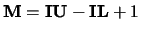 .
.
- IFAIL
- Optional (output) INTEGER array,
shape
 with
with 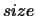 (IFAIL)
(IFAIL) 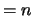 .
.
If INFO 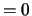 , the first M elements of IFAIL are zero.
, the first M elements of IFAIL are zero.
If INFO 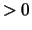 , then IFAIL contains the indices of the
eigenvectors that failed to converge.
Note: If Z is present then IFAIL should also be present.
, then IFAIL contains the indices of the
eigenvectors that failed to converge.
Note: If Z is present then IFAIL should also be present.
- Q
- Optional (output) REAL or
COMPLEX square array, shape(:,:) with
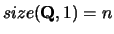 .
.
If Z is present, the matrix used in the reduction of
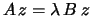 to tridiagonal form.
to tridiagonal form.
- ABSTOL
- Optional (input) REAL.
The absolute error tolerance for the eigenvalues.
An approximate eigenvalue is accepted as converged
when it is determined to lie in an interval ![$[a,b]$](img624.gif) of width less than or equal to
of width less than or equal to
where wp is the working precision. If ABSTOL 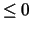 ,
then
,
then
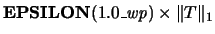 will be used in its place,
where
will be used in its place,
where 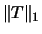 is the
is the 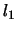 norm of the tridiagonal matrix
obtained by reducing the generalized eigenvalue problem to tridiagonal form.
Eigenvalues will be computed most accurately when ABSTOL is
set to twice the underflow threshold
norm of the tridiagonal matrix
obtained by reducing the generalized eigenvalue problem to tridiagonal form.
Eigenvalues will be computed most accurately when ABSTOL is
set to twice the underflow threshold
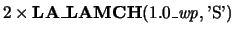 , not zero.
, not zero.
Default value: 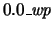 .
.
Note: If this routine returns with
 , then some
eigenvectors did not converge. Try setting ABSTOL to
, then some
eigenvectors did not converge. Try setting ABSTOL to
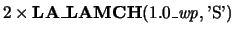 .
.
- INFO
- Optional (output) INTEGER.
![\begin{infoarg}
\item[{$= 0$:}] successful exit.
\item[{$< 0$:}] if {\bf INFO}...
...d and
no eigenvalues or eigenvectors were computed.
\end{infoarg}\end{infoarg}](img855.gif)
If INFO is not present and an error occurs, then the
program is terminated with an error message.
References: [1] and [17,9,20,21].





Next: Example (from Program LA_SBGVX_EXAMPLE)
Up: Generalized Symmetric Eigenvalue Problems
Previous: Purpose
Contents
Index
Susan Blackford
2001-08-19
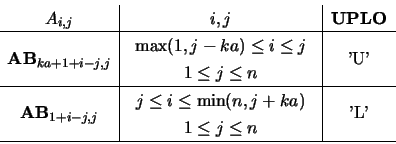
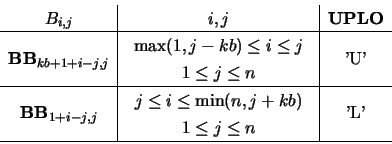
![\begin{optionarg}
\item[{$ =$\ 'U':}] Upper triangles of $A$\ and $B$\ are stor...
...item[{$ =$\ 'L':}] Lower triangles of $A$\ and $B$\ are stored.
\end{optionarg}](img791.gif)
![\begin{infoarg}
\item[{$= 0$:}] successful exit.
\item[{$< 0$:}] if {\bf INFO}...
...d and
no eigenvalues or eigenvectors were computed.
\end{infoarg}\end{infoarg}](img855.gif)